Liczby rządzą światem – co do tego nikt nie ma wątpliwości. Są wszędzie wokół nas a matematyka aż roi się od mniej i bardziej egzotycznych ich odmian. Każdy przeciętny człowiek wysiada już przy liczbach niewymiernych – π i √2 wystarczają nam z nawiązką i nikomu nie chce się zagłębiać stałej Eulera (znienawidzone przez wszystkich e z logarytmu naturalnego) czy stałej Feigenbauma (opisującej chaos deterministyczny i coś, co jest bolączką drugorocznych studentów na ćwiczeniach z biofizyki – bifurkację). Jakby nie było tego dość, matematycy serwują nam coraz to nowe rozszerzenia zbioru liczb, których stosunkowo jeszcze łagodnymi przedstawicielami są liczby zespolone (któż nie słyszał o sławetnym pierwiastku z -1…)

Ale liczby to nie tylko matematyka – a raczej to nie tylko matematyczny formalizm. Idąc za redukcjonistami, to matematyka jest tym, co kryje się za zasłoną całego otaczającego nas świata. Jest silnikiem rzeczywistości i motorem wszelkiej akcji, jaką zna świat, tak ożywiony jak i nieożywiony. Brzmi to trywialnie – ale liczby tworzą rzeczywistość. Problem w tym, że generalnie bierzemy ich obecność na wiarę, podświadomie przyjmujemy ich własności. Często podejrzewamy, że jakaś złożona struktura matematyczna kryje się za liczbowym rusztowaniem przyrody – ale nie potrafimy tego zdefiniować, opisać. Gdzie one zatem są, owe liczby? Czy możemy dostrzec w ich chaosie porządek natury? A może na odwrót – dostrzec w chaosie natury harmonię liczb? 

Niejednokrotnie wykształcanie się określonych cech organizmów żywych na bazie pewnych wzorców liczbowych jest determinowane doskonale znaną z ewolucji optymalizacją. Mówiąc ogólnie i prosto – optymalizacja to próba znalezienia kompromisu, odszukania takiej zależności między czynnikami, która pozwoli maksymalizować zysk (np. związany z sukcesem reprodukcyjnym czy korzyścią energetyczną) lub też zminimalizować koszty danej czynności. Często jednak trudno jest odszukać w prawidłowościach natury głębsze relacje i doszukać się funkcji określonych wzorców.

Jednym z najsłynniejszych liczbowych kawałków rzeczywistości jest ciąg Fibonacciego. Nazwisko tego włoskiego uczonego – naprawdę zwącego się Leonardem z Pizy – kojarzy się praktycznie każdemu, ale już na pytanie dotyczące jego wkładu w rozwój nauki niewielu zna odpowiedź. A Fibonacci odegrał naprawdę istotną rolę w rozwoju matematyki. Przede wszystkim, jako jeden z pierwszych średniowiecznych uczonych, upowszechnił arabski system zapisu liczb, tak dobrze znany nam z codziennego życia. Nie z tego jednak Fibonacci słynie – w historii nauki zapisał się bowiem dzięki pewnemu myślowemu eksperymentowi z królikami…

Załóżmy że mamy płodną parę królików. Są to specjalne króliki – żyją bowiem wiecznie. Nasza para wydaje potomstwo w postaci nowej pary królików. Każdy nowy królik nabiera zdolności do rozrodu dopiero w drugim miesiącu życia. Innym słowem w miesiącu pierwszym była jedna para, w drugim dwie (jedna nowa), a trzecim trzy (gdyż ta nowa jeszcze nie mogła się rozmnażać). W kolejnym miesiącu będzie pięć par (gdyż już dwie będą mogły się rozmnażać, a zostanie też dodatkowa, niedojrzała para „nowa”). Rozwijając króliczą historię dochodzimy do dość dużych liczebności – nie to jednak jest sednem sprawy. Liczby królików w kolejnych pokoleniach układają się w pewien ciąg: 1, 2, 3, 5, 8, 13… Każda kolejna liczba w tym ciągu jest sumą dwóch poprzednich, lub, ogólnie:

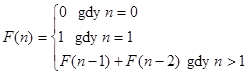
Taki ciąg liczbowy znany jest właśnie jako ciąg Fibonacciego. Nietrudno zauważyć, że podany myślowy eksperyment jest dość mało realny. Szczególnie jeśli chodzi o założenie o nieśmiertelności osobników – dość niebezpieczne biorąc pod uwagę tempo rozrodu królików 😉 („ledwo” 28. liczba ciągu to 19641…). Ale są prawdziwe organizmy o rozrodzie rządzonym – przynajmniej w zarysie – ciągiem Fibonacciego. Mowa o pszczołach Apis mellifera. Doskonale wiadomo, że samce pszczół – trutnie – powstają z niezapłodnionych jaj, co oznacza, że mają tylko jednego rodzica (matkę – królową). Samice mają dwoje rodziców – królową oraz trutnia. Gdyby narysować drzewo genealogiczne takich osobników – samic i samców – okaże się, że rządzą nim liczby Fibonacciego. I tak: samiec ma 1 rodzica (matkę), 2 dziadków, 3 pradziadków, 5 prapradziadków; samica z kolei ma 2 rodziców, 3 dziadków, 5 pradziadków oraz 8 prapradziadków – itd. Wymienione liczby to oczywiście elementy ciągu Fibonacciego.

Ale ciąg Fibonacciego znajduje zastosowanie w znacznie bardziej wyrafinowanych „konstrukcjach” przyrody – i jest tam doskonale zamaskowany. Spróbujmy na przykład wykonać taką konstrukcję: dany jest kwadrat o boku 1. Wrysujmy w niego łuk koła o promieniu równym bokowi kwadratu. Następnie dobudujmy kwadrat o boku równym poprzedniego (czyli znów 1) i kontynuujmy rysowaniu łuku. Powstał prostokąt o bokach 2:1. Dobudujmy na dłuższym boku kwadrat o boku 2 i wrysujmy w niego ciąg dalszy krzywej – tyle że teraz będzie to łuk koła o promieniu 2. Do tak powstałego prostokąta o boku 2:3 dobudujmy kwadrat o boku 3 i powtórzmy rysowanie łuku. Postępując tak dalej (kolejne dobudowywane kwadraty będą miały boki 5, 8, 13 itd.) otrzymamy spiralę, określaną czasem jako spirala Fibonacciego, albo też jako spirala logarytmiczna. Okazuje się, że nader często. Tego typu kształt występuje w przyrodzie. Najdoskonalszym przykładem jest przepiękna muszla głowonoga morskiego łodzika Nautilus sp. Na jej przekroju poprzecznym widzimy w stanie niemalże doskonałym ową spiralę. Ale to nie koniec. Spirala Fibonacciego spotykana jest w wielu innych miejscach. Ślimak ucha wewnętrznego człowieka jest również przykładem prawie doskonałej spirali logarytmicznej. Czy to koniec? Oczywiście, że nie.

Innym doskonale znanym przykładem występowania liczb Fibonacciego jest ulistnienie skrętoległego skrętoległego roślin. Weźmy łodygę gatunku o takim ulistnieniu i policzmy którym z kolei liściem na łodydze jest liść leżącym dokładnie nad dowolnym innym liściem (nazwijmy go zerowym). Okaże się, że zawsze będzie to liczba z ciągu Fibonacciego (np. 8). Co więcej liczba skrętów ulistnienia od tego zerowego liścia do leżącego dokładnie nad nim (np. 5) będzie zawsze równa liczbie sąsiadującej w ciągu Fibonacciego z poprzednią (lub odległej o co najwyżej 2 pozycje). Często zapisuje się je w postaci ułamka, opisującego ulistnienie – tutaj miałby on wartość 5/8. Stosunek ten jest stały i charakterystyczny dla gatunku – dla przykładu wiąz, cytryna, trawy mają stosunek ½; dąb wiśnia, jabłko – 2/5; topola, róża, wierzba 3/8; migdałowiec – 5/13.

Zdaje się być generalną regułą, że wzrostem roślin rządzi ciąg Fibonacciego. W kwiatach roślin z rodziny złożonych Asteraceae kwiaty rurkowate upakowane są charakterystyczne „łuki”. Okazuje się, że liczby łuków liczonych w prawo oraz w lewo są sąsiadującymi ze sobą liczbami ciągu Fibonacciego. Podobna relacja występuje np. w ustawieniu łusek w szyszkach roślin nagonasiennych. W gruncie rzeczy nie powinno nas to dziwić – kwiaty czy łuski nasienne to przekształcone liście, a liście – jak wiemy –wiernie poddają się Fibonacciemu. Pytanie jednak – skąd tego typu zależności się biorą? Czy takie upakowanie jest optymalne i wystarczająco trwałe (jak sugerują niektórzy)? Czy może w kodzie genetycznym z jakichś powodów rozwój wg ciągu Fibonacciego jest faworyzowany nad innymi wzorcami? Jak dotąd nikt nie podał zadowalającej odpowiedzi na wszechobecność tego modelu wzrostu.

Częściową odpowiedź daje jednak matematyka. Już starożytni Grecy wiedzieli jak ważna jest estetyka proporcji. Zresztą to oni dostrzegli regularność w idealnie zbudowanym ludzkim ciele. Potrafili tą doskonałość zastosować w budownictwie – budownictwie tym zyskali sobie sławę architektów doskonałych. Jednym z wynalazków starożytnych jest tzw. Złoty podział – podział odcinka na takie dwa fragmenty, że stosunek długości części dłuższej do krótszej jest taki jak stosunek długości całego odcinka do części dłuższej. Stosunek ten, będący rozwiązaniem równania kwadratowego (nie będę zamęczał czytelnika jego rozwiązaniem…) to właśnie tak zwana złota liczba – w przybliżeniu 1.62, dokładnie zaś:

Złota liczba ma wiele ciekawych własności – np.: 1/φ = 1 – φ. Przede wszystkim jednak złota liczba okazała się być najoptymalniejszym sposobem upakowywania rosnących osiowo obiektów (np. liści, łusek). Okazuje się, że wzrost z obrotem w każdym następnym podziale o pewien kąt jest optymalny, ale – co już nie jest do końca trywialne – najoptymalniejsze upakowanie rosnących elementów (bez nadmiernego „ścisku” oraz z wykorzystaniem całej wolnej przestrzeni) uzyskuje się dopiero w sytuacji, gdy na jeden obrót w czasie wzrostu przypada dokładnie φ liści/łusek/kwiatów/nasion… Wtedy mamy do czynienia z ustawieniem naprawdę dobrym – np. liście zacieniają się w możliwie najmniejszym stopniu, pozwalając też wodzie deszczowej spływać w okolice korzeni. Najciekawsze jednak jest, że ową liczbę 1/φ najlepiej aproksymuje (matematyk by powiedział, że liczba ta jest granicą pewnego ciągu) ciąg ilorazów sąsiednich liczb ciągu Fibonacciego. Okazuje się więc, że liczby Fibonacciego są najlepszymi całkowitymi przybliżeniami stosunków optymalnych w roślinie, wynikających ze złotego podziału.

Złoty podział występuje nie tylko w roślinach. Dostrzeżono go w bardzo wielu miejscach. Ludzkie ciało i twarz są zbudowane wg proporcji określonych różnymi potęgami liczby φ. Złoty podział dostrzeżono nawet w materiale genetycznym – okazuje się, że helisa DNA ma strukturę w której doszukać się można złotego podziału (dokładnie złotego prostokąta).

Porządek wyłania się nawet w pozornie tak chaotycznym miejscu jak kipiący tygiel życia. Nawet tutaj matematyka pokazuje, że to on wszystkim zawiaduje. A pokazuje to w sposób bardzo ciekawy, żeby nie powiedzieć urzekający… W następnych numerach pisma spróbujemy się przyjrzeć innym zjawiskom liczbowym w naturze – takim jak fenomen liczb pierwszych czy struktury fraktalne.

Autor: Szymon Drobniak 

Referencje:

http://en.wikipedia.org/wiki/Fibonacci
http://www.stangrist.com/fibonacci.htm