Mathematics hidden in nature
22 October 2014
Numbers rule the world – there is no doubt about it. They are all around us and mathematics swarms with their less and more exotic types. Any average person already gives up when it comes to irrational numbers – π and √2 suffice for us and nobody feels like studying Euler’s constant (the commonly hated base of the natural logarithm) or Feigenbaum constant (describing deterministic chaos, as well as the nightmare of second year students in biophysics classes – bifurcation). And as if that was not enough, mathematicians keep giving us new extensions of the set of numbers whose relatively harmless representatives are complex numbers (everyone must have heard of the famous root of -1…)
But numbers are present not only in mathematics – or rather, not only in mathematical formulas. According to reductionists, mathematics is what hides behind the veil of the world around us. It is the motor of reality and the motor of all action known to the world, both animate and inanimate. This sounds trivial – but numbers create reality. The problem is that we generally merely believe in their presence and subconsciously assume their properties. We frequently suspect that some complex mathematical structure must hide behind the numerical scaffolding of nature – but we cannot define or describe how exactly. So where are they, the numbers? Can we see the order of nature in their chaos? Or vice versa – see the harmony of numbers in the chaos of nature?
Frequently, the development of particular traits in living organisms based on numerical patterns is determined by optimisation, a rule so common in evolution. To put it in general and simple terms – optimisation is an attempt at finding a compromise, a relation between factors allowing to maximise the benefits (e.g. connected with reproductive success or energy benefits) or minimise the costs of a given activity. But it is often difficult to find deeper relations in the regularities observed in nature, or discover the function of specific patterns.
Assume that we have a fertile pair of rabbits. These are special rabbits – because they live forever.
The couple has offspring – a pair of new rabbits. Each new rabbit can mate only in the second month of its life. In other words: in the first month there is only one couple, in the second month there are two couples (one new), in the third month three couples (as the new one could not reproduce yet). In the consecutive month there will be five pairs (as two pairs would already be able to mate, and there will be a “new”, immature pair). As the rabbit history develops, we achieve quite a large population – this, however, is not important here. The numbers of rabbits in consecutive generations form a certain sequence: 1, 2, 3, 5, 8, 13… Each successive number in the sequence is a sum of the two preceding numbers, or, generally:
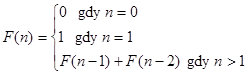
This sequence of numbers is known as the Fibonacci sequence. It is not difficult to realise that the provided thought experiment is rather not probable. Especially when it comes to assumption concerning immortality of individuals – it is quite dangerous, taking into consideration the pace of rabbit reproduction 😉 (“scarcely” 28th number of the sequence is 19641…). But actual organisms that reproduce according to the Fibonacci sequence – at least in general – do exist. We are talking about Apis mellifera honey bees.
It is generally known that male bees – drones – are the product of an unfertilised egg. It means that they have only one parent (the mother – the queen). Females have two parents – the queen and a drone.
If you draw a family tree of such individuals – females and males – it turns out it is governed by Fibonacci numbers. A male has 1 parent (a mother), 2 grandparents, 3 great grandparents, 5 great great grandparents; a female, on the other hand, has 2 parents, 3 grandparents, 5 great grandparents and 8 great great grandparents etc. These numbers, of course, form a Fibonacci sequence.
But the Fibonacci sequence finds its application in much more sophisticated natural “structures” – and is perfectly concealed in them. Let’s try to create the following structure: we start with a square with side length 1. Let’s inscribe into it an arc with a radius equal to the side of the square.
Then, let’s add a square with the side equal to the previous one (i.e. 1 again) and continue drawing the arc. We get a rectangle with sides 2:1. At the longer side let’s add a square with the side equal 2 and inscribe into it a continuation of the curve – only this time it will be an arc of a circle with a radius equal to 2.
To the resulting rectangle with sides 2:3 let’s add a square with side 3 and repeat the process of drawing the arc. By repeating the steps (the subsequently added squares will have the sides of 5, 8, 13 etc.) we will get a spiral, sometimes called a Fibonacci spiral, or logarithmic spiral. It turns out that shapes of this type
appear in nature very frequently. The best example is the beautiful shell of the sea cephalopod Nautilus sp. In its cross section we can see an almost perfect example of the spiral. But that is not all. The Fibonacci spiral can also be found in many other places. The inner ear cochlea in humans is also an example of an almost perfect logarithmic spiral. Is that all? Of course not.
Another well-known example of Fibonacci numbers’ presence in nature is the spiral leaf pattern (phyllotaxis) in plants.
Let’s take a stem of a species with such phyllotaxis and count which consecutive leaf on the stem is located exactly above some other leaf (let’s call it leaf zero).
It turns out that it will be always a number from Fibonacci sequence (e.g. 8). What’s more, the number of full turns between such a leaf zero and the leaf located directly above it (e.g.5) will always be equal to the number adjacent in Fibonacci sequence to that former number (or moved from it no further than by 2 positions in the sequence). It is frequently expressed as a fraction describing the phyllotaxis – here it would take the value 5/8. The ratio is constant and characteristic for particular species – for example for elm, lemon, grasses, the ratio is 1/2; for oak, cherry, apple – 2/5; for poplar, rose, willow 3/8; for almond – 5/13.
It seems that as a general rule, plant growth is governed by Fibonacci sequence. The tubular flowers of plants of the Asteraceae family are packed into characteristic “arcs”. It turns out that the number of arcs counted to the right and to the left are the numbers adjacent in Fibonacci sequence. A similar relation is found, for example, in the arrangement of scales in the gymnosperms’ cones. This, actually, should not surprise us: flowers or seed scales are transformed leaves, and leaves – as we know – minutely abide by the Fibonacci’s principles. However, the question is – where do those relations come from? Is such packing the most optimal and sufficiently resistant (as some suggest)? Or perhaps, the development according to Fibonacci sequence is for some reasons favoured over other patterns in the genetic code? So far no-one has given a sufficient explanation to the ubiquity of this growth pattern.
Mathematics, however, gives us a partial answer. The importance of the aesthetics of proportions was already known to ancient Greeks. It was they who noticed the regularity in the perfect construction of the human body. They could use that perfection in their buildings – which made them famous for being excellent architects. One of the ancient inventions was the so-called Golden ratio – a division of a segment into two parts, one longer than the other, whose ratio is the same as the ratio of the whole length to the length of the longer part. The ratio, which is approximately the solution to a quadratic equation (I will not bore the reader with actually solving it here…) is exactly the so-called golden number – approximately 1.62, and precisely:
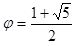
The golden number has many interesting properties – e.g.: 1/φ = 1 – φ. But most importantly, the golden number turned out to be the most optimal way of packing axially growing objects (e.g. leaves, scales). It turns out that growth involving rotation by a certain angle in each subsequent division is optimal, but – what is not so trivial – the most optimal packing of growing elements (without excessive “squeezing” and while using all the available space) is obtained only when there is exactly φ leaves/scales/flowers/seeds per one turn during growth … Then the arrangement is really good – e.g. the leaves shade each other as little as possible, allowing the rainwater to flow down towards the roots. The most interesting part, however, is that the 1/φ number is most closely approximated (a mathematician would say that the number is the limit of a certain sequence) by a sequence of quotients of adjacent numbers in the Fibonacci sequence. It turns out that Fibonacci numbers are the best integer approximation of optimal ratios in a plant, resulting from the golden ratio.
The golden ratio appears not only in plants; it is seen in multitude of places. The human body and face follow the proportions resulting from various powers of φ. The golden ratio is discovered even in genetic material – it turns out that the golden section (a golden rectangle, to be specific) can be found in the structure of DNA helix.